Hay problemas en los que ordenar los datos de entrada es crucial para poder resolverlos. Como algunos de ustedes sabrán, python tiene un algoritmo poderoso de ordenamiento para listas, que actúa como un método sobre estas, en efecto, dada cualquier lista de números, p.e.,
Lista=[0, 1, 2, 2, 3, 3, 4, 4, 5, 6, 6, 6, 7, 8, 8, 9, 11, 13, 22]
podemos ordenarla simplemente colocando:
Lista.sort()
Ahora bien, aunque posiblemente este método sobre listas sea la mejor opción para ordenarlas, cuando las entradas de la lista son números, no pasa lo mismo cuando son objetos no numéricos, ordenados mediante alguna función u orden parcial. Les daré un ejemplo que puede que les sea útil.
Supongamos que tenemos una lista de listas, dada por:
Lista2=[[1, 200, 50000],[1,2,3],[1],[100],[2,2,3,4,5,6,3,21],[1,2,5,2,5,7],[1,2,0,8,7,6],[5,6,4,8,3,2],[2,3],[1,2,99]]
y el orden parcial (o score), venga dado por, por ejemplo, el promedio de los valores de las entradas. ¿Podremos usar el método sort en esta lista?, la respuesta es claramente no. Este ordenará la lista utilizando la primera entrada en cada lista como referencia, lo cual no nos permitirá aplicar nuestro orden especial.
Solución:
Implementé el algoritmo de ordenamiento de burbuja (el cual es uno de los más fáciles), para resolver esta cuestión.
Pseudo-Código (Algoritmo de la Burbuja):
Una animación que clarifica bastante la forma en la que este algoritmo trabaja puede verse a continuación:
haga click en la imagen
El código:
### copia desde aquí ###
### copia desde aquí ###
def orden(E):
n=len(E)
score=0
for i in E:
score=score+i
score=float(score)/n
return score
def ordenamiento(L):
n=len(L)
for i in range(1, n):
for j in range(n-i):
if orden(L[j])>orden(L[j+1]):
L[j], L[j+1]=L[j+1], L[j]
return L
# y ordenamos
Lista2=ordenamiento(Lista2)
### fin del algoritmo ###
Si aún no estas convencido de porque un algoritmo de orden flexible (como este) es importante y útil, no solo en programación, sino en ciencias en general, enunciaré un par de aplicaciones en las que ordenar puede ser crucial:
- Problemas de organización de tareas: Puede que necesites automatizar la realización de tareas, por una maquina, o por personas, y necesites hacerlo de la mejor forma, tomando en cuenta por ejemplo, la prioridad, o las dependencias intra-tareas. En este caso, los ordenes son especiales, y los tipos de datos de entrada no son a priori números.
- Análisis de Propagación: Dado el origen de una enfermedad en una ciudad, y como datos, todas las ciudades circunvecinas, y como meta-datos las distancias y la cantidad promedio de flujo de personas intra-ciudades. Podemos usar un algoritmo como el explicado, para las ciudades por el riesgo de adquirir la enfermedad, donde dicho riesgo es una función de los datos y los meta-datos.
- Y existen muchos mas ejemplos ... creo que en este punto, las palabras sobran, sino, ordena los siguientes libros por temática:
Saludos.
Si te ha gustado este artículo, compártelo en facebook, twitter, google+, coméntalo, envíalo por correo, y si quieres mas información, pídela. Si no te gusta, critícalo. Tu tienes completo control sobre los contenidos de este blog.

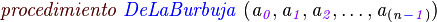


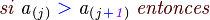

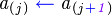

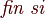

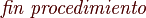


No hay comentarios:
Publicar un comentario