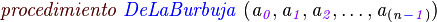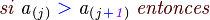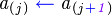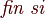Me encuentro escribiendo grandes e interesantes noticias para este blog, luego de un tiempo de profunda meditación :-)

En los próximos días se publicarán varias.

¡ Salud !

Utilidad: ¿Necesitas imprimir dos páginas por hoja a dos caras?

En estos días necesitaba imprimir un artículo suficientemente voluminoso como para pensar imprimir dos páginas por hoja, pero a su vez, no quería gastar mas hojas de las necesarias (hay que ahorrar, la naturaleza lo agradecerá). Pues bien, escribí un pequeño código para separar las páginas de manera que 1,2 quedarán en la primera página, 2,3 en la otra cara, 5,6 en la segunda página, 7,8 en la otra cara, y así sucesivamente. Como mi impresora no imprime a dos caras, tuve que imprimir primero una lista y luego la otra.

Para ello necesitaría dos sucesiones, una que me imprimiera las caras frontales, y la otra que hiciera el trabajo con las traseras. A continuación dejo el código, las matemáticas detrás de este son tan básicas que no vale la pena explicarlas :-)

 # -*- coding: utf-8 -*-
"""
@author: Alejandro Alvarez
"""

NPAG=200 # Número de páginas

I1=[]
I2=[]
for n in range(int(NPAG/4.0)):
    I1.append(4*n+1)
    I1.append(4*n+2)
    I2.append(4*n+3)
    I2.append(4*n+4)

print "Primera Impresion:"
print I1
print
print
print "Segunda Impresion:"
print I2

El código corriendo en spyder:

Espero que les sea de utilidad.

Nota corta: Una guía de programación orientada a objetos con Python

Buscando información sobre el uso de distintos paradigmas para simplificar mi vida como programador me encontré con el siguiente mini-tutorial, el cual considero bastante bueno como para recomendarlo.

Version Online

http://blog.rvburke.com/2006/11/22/programacion-orientada-a-objetos-en-python/

Version en PDF

http://blog.rvburke.com/wp-content/uploads/2006/11/Introducci%C3%B3n-a-la-programaci%C3%B3n-orientada-a-objetos.pdf

Espero que lo disfruten.

Distribuciones Aleatorias con Python: Parte I

Es bien sabido que python posee una poderosa librería para generar números y distribuciones aleatorias. En este post explicaremos como generar números que siguen una distribución uniforme, una distribución gaussiana o normal y una distribución de pareto.

Adicionalmente, utilizaremos parte de lo aprendido en el post:

Histogramas con Python + Matplotlib  

para graficar los histogramas de los datos generados.

Necesitaremos tener instalada la librería matplotlib, y utilizaremos adicionalmente la librería random que biene por defecto con python.

Pasamos entonces a mirar el código que nos permitirá hacer todo lo comentado anteriormente:

# -*- coding: utf-8 -*-

"""

Creado por: Alejandro J. Alvarez S.

19 de Junio de 2012

"""

import random as r

from matplotlib.pylab import hist, show, figure

uniforme=[] # Distribución uniforme entre 0 y 1

gaussiana=[] # Distribución Gaussiana, con centro 0 y desviación estándar 1

pareto=[] # Distribución de pareto, con parametro de forma alpha=3/2

numiter=100000

bins=100

for i in range(numiter):

uniforme.append(r.uniform(0,1))

gaussiana.append(r.gauss(0,1))

pareto.append(r.paretovariate(2.5))

figure()

h1=hist(uniforme,bins)

figure()

h2=hist(gaussiana,bins)

figure()

h3=hist(pareto,bins,(0,10))

show()

Observese que se crearon tres listas para guardar los numeros que siguen los tres tipos de distribuciones que deseamos simular. numiter es el número de iterados y bins, es el numero de partes en las que dividiremos el espacio muestral. Finalmente se crean tres figuras a partir de la data generada con el comando hist. por último, utilizamos la instrucción show() para mostrar en pantalla cada una de las figuras.

El resultado final es el siguiente:

Espero que este post les sea de utilidad.

Si te ha gustado este artículo, compártelo en facebook, twitter, google+, coméntalo, envíalo por correo, y si quieres mas información, pídela. Si no te gusta, critícalo. Tu tienes completo control sobre los contenidos de este blog.

Calculando factores primos con Sympy

Sympy es una mega-librería de matemáticas para python, en ella podrás encontrar funciones para integrar simbólicamente, generadores de polinomios especiales, rutinas para resolver analítica y numéricamente ecuaciones diferenciales, y mucho más.

En nuestro caso estaremos interesados en la sub-libreria de teoría de números ntheory. En esta podremos encontrar entre otras cosas una función que calcula todos los factores primos de un número.

Ejemplo 1:
Como objetivo inicial fijémonos como meta calcular los factores primos del número 13195.

El programa iniciaría de la siguiente forma


# -*- coding: utf-8 -*-
from sympy.ntheory import primefactors as pf
# hemos cargado la función que calcula los factores primos de un número.
print pf(13195)
# Programa Finalizado


El resultado final será la lista:

[5, 7, 13, 29]


para aumentar la complejidad de nuestro programa, resolvamos el siguiente problema.

Problema 1:
Consideremos el siguiente número entero:

374874837483748738478374837473

calcular la suma de todos sus factores primos.

Solución: El preámbulo del programa anterior nos servirá mucho para esta tarea.

# -*- coding: utf-8 -*-
from sympy.ntheory import primefactors as pf
L=pf(374874837483748738478374837473)
suma=0
for i in L:
    suma=suma+i
print “El resultado es: ”, suma
# fin del programa


El resultado final fue:

51906840377


Solo me queda decirles ... Que se diviertan :-)

Si te ha gustado este artículo, compártelo en facebook, twitter, google+, coméntalo, envíalo por correo, y si quieres mas información, pídela. Si no te gusta, critícalo. Tu tienes completo control sobre los contenidos de este blog.

Algoritmos de Ordenamiento en Python: El método de la Burbuja

Hay problemas en los que ordenar los datos de entrada es crucial para poder resolverlos. Como algunos de ustedes sabrán, python tiene un algoritmo poderoso de ordenamiento para listas, que actúa como un método sobre estas, en efecto, dada cualquier lista de números, p.e.,

Lista=[0, 1, 2, 2, 3, 3, 4, 4, 5, 6, 6, 6, 7, 8, 8, 9, 11, 13, 22]

podemos ordenarla simplemente colocando:

Lista.sort()

Ahora bien, aunque posiblemente este método sobre listas sea la mejor opción para ordenarlas, cuando las entradas de la lista son números, no pasa lo mismo cuando son objetos no numéricos, ordenados mediante alguna función u orden parcial. Les daré un ejemplo que puede que les sea útil.

Supongamos que tenemos una lista de listas, dada por:

Lista2=[[1, 200, 50000],[1,2,3],[1],[100],[2,2,3,4,5,6,3,21],[1,2,5,2,5,7],[1,2,0,8,7,6],[5,6,4,8,3,2],[2,3],[1,2,99]]

y el orden parcial (o score), venga dado por, por ejemplo, el promedio de los valores de las entradas. ¿Podremos usar el método sort en esta lista?, la respuesta es claramente no. Este ordenará la lista utilizando la primera entrada en cada lista como referencia, lo cual no nos permitirá aplicar nuestro orden especial.

Solución:

Implementé el algoritmo de ordenamiento de burbuja (el cual es uno de los más fáciles), para resolver esta cuestión.

Pseudo-Código (Algoritmo de la Burbuja):

Una animación que clarifica bastante la forma en la que este algoritmo trabaja puede verse a continuación:

haga click en la imagen

El código:
### copia desde aquí ###

def orden(E):

    n=len(E)

    score=0

    for i in E:

        score=score+i

    score=float(score)/n

    return score

def ordenamiento(L):

    n=len(L)

    for i in range(1, n):

        for j in range(n-i):

            if orden(L[j])>orden(L[j+1]):

                L[j], L[j+1]=L[j+1], L[j]

    return L

# y ordenamos

Lista2=ordenamiento(Lista2)

### fin del algoritmo ###

Si aún no estas convencido de porque un algoritmo de orden flexible (como este) es importante y útil, no solo en programación, sino en ciencias en general, enunciaré un par de aplicaciones en las que ordenar puede ser crucial:

• Problemas de organización de tareas: Puede que necesites automatizar la realización de tareas, por una maquina, o por personas, y necesites hacerlo de la mejor forma, tomando en cuenta por ejemplo, la prioridad, o las dependencias intra-tareas. En este caso, los ordenes son especiales, y los tipos de datos de entrada no son a priori números.
  
  
• Análisis de Propagación: Dado el origen de una enfermedad en una ciudad, y como datos, todas las ciudades circunvecinas, y como meta-datos las distancias y la cantidad promedio de flujo de personas intra-ciudades. Podemos usar un algoritmo como el explicado, para las ciudades por el riesgo de adquirir la enfermedad, donde dicho riesgo es una función de los datos y los meta-datos.
  
• Y existen muchos mas ejemplos ... creo que en este punto, las palabras sobran, sino, ordena los siguientes libros por temática:

Saludos.

Si te ha gustado este artículo, compártelo en facebook, twitter, google+, coméntalo, envíalo por correo, y si quieres mas información, pídela. Si no te gusta, critícalo. Tu tienes completo control sobre los contenidos de este blog.

Histogramas con Python + Matplotlib

Uno de los paquetes mas completos para graficar con Python es Matplotlib. El día de hoy explicaré como graficar un histograma sencillo utilizando el sub-paquete pylab y las funciones hist y show.

import random
from matplotlib.pylab import hist, show
v=range(0,21)
data=[]
for i in range(1000):
    data.append(random.choice(v))

hist(data,21, (0,20))
show()

Resultado

Explicación linea a linea

Linea 1.  import random

Importamos el paquete random para generar datos de manera aleatoria para el histograma.

Linea 2. from matplotlib.pylab import hist, show

Del subpaquete pylab de matplotlib importamos las funciones hist y show. La función hist es la que crea los datos del histograma, y show muestra en pantalla dicho histograma.

Linea 3. v=range(0,21)

Creamos un vector de posibles resultados del experimento, es decir, en nuestro experimento, los posibles resultados varían entre 0 y 20 (en total 21 datos posibles).

Linea 4. data=[]

Se crea una lista donde guardaremos la frecuencia en la que aparece cada uno de los posibles resultados del experimento.

Linea 5 y 6.
for i in range(1000):
____data.append(random.choice(v))

Generamos los datos de nuestro experimento. Para ello hacemos una elección aleatoria de los posibles resultados de nuestro experimento. En nuestro caso, se está realizando el experimento en el que se elige mil veces un número entre 0 y 20, en cada extracción se repone el número elegido y la probabilidad de elegir cada uno de los números es la misma. Dicho de otra forma, la distribución de probabilidad es uniforme.

Linea 7. hist(data,21, (0,20))

Generamos el histograma con la función hist. Observar que los argumentos de la función hist son: los datos, la cantidad de diferentes valores del experimento, y el rango de dichos valores. 

Linea 8. show()

Por último, usamos el comando show() para graficar el histograma generado.

Si te ha gustado este artículo, compártelo en facebook, twitter, google+, coméntalo, envíalo por correo, y si quieres mas información, pídela. Si no te gusta, critícalo. Tu tienes completo control sobre los contenidos de este blog.